В. В. Осипов, В. П. Пономаренко, А. Ю. Селяков
Государственное унитарное предприятие “Научно-производственное объединение “Орион”
Москва, Россия
Рассмотрена физика работы новой смотрящей ИК гибридной матрицы на основе HgCdTe р-n-переходов. Проанализированы предельные пороговые характеристики таких матриц на спектральные диапазоны 3 - 5 и 8 - 14 мкм. Архитектура рассматриваемых матриц намного проще чем у существующих: накопительные емкости занимают всю площадь под фоточувствительной ячейкой, а в качестве элементов коммутации используются сами фоточувствительные р-n-переходы. Накопительные емкости могут быть изготовлены на основе диэлектриков с относительно высокой диэлектрической проницаемостью (типа TiO2 и интегрированных сегнетоэлектриков). В отличие от фото-ПЗС и -ПЗИ, в рассматриваемой матрице не используется перенос заряда между пространственно разнесенными электродами. Определены параметры фоточувствительных и накопительных элементов, при которых реализуются наибольшие времена накопления и пороговые характеристики, близкие к теоретическому пределу. Показано, что в принципе рассматриваемая матрица обладает уникальными параметрами и в ней могут быть подавлены шумы усилителя типа 1/f. Так, матрицы, площадь фоточувствительного р-n-перехода которых составляет 20х20 мкм2, могут работать в BLIP-режиме и иметь время накопления фотосигнала и формат, равные постоянной времени человеческого глаза и 1024х1024 элементов для диапазона 3 - 5 мкм и, соответственно, 300 мкс и 256х256 элементов для диапазона 8–10 мкм при температуре фона 300 К.
1. Введение
Одним из основных направлений развития современной инфракрасной (ИК) техники является создание смотрящих матриц большого формата на спектральные диапазоны 3-5 и 8-14 мкм. Тепловизоры на основе таких матриц не требуют оптического сканирования при формировании сигнала изображения и должны реализовывать преимущества обработки фотосигнала, связанные с большим временем его накопления. Последнее в пределе может быть равно времени кадра, которое, как правило, определяется инерционностью человеческого глаза.
К настоящему времени реализованы крупноформатные гибридные фокальные матрицы различного типа [1], в том числе на основе узкозонных полупроводников HgCdTe [2-5] и InSb [6], а также квантоворазмерных гетероструктур GaAs/AlGaAs [7, 8]. В таких приборах матрица фоточувствительных элементов из соответствующего полупроводника соединяется с помощью индиевых столбиков с кремниевой микросхемой, выполняющей функции накопления, усиления и коммутации фотосигнала. Созданы также планарные матрицы на основе фотодиодов Шоттки из PtSi [9] и гетеропереходов GeSi/Si [10], объединенных с элементами обработки сигнала на единой кремниевой подложке. Разработаны крупноформатные неохлаждаемые болометрические матрицы [11]. Предпринимаются попытки создания перспективных для ИК-матриц фотодетекторов на основе квантоворазмерных гетероструктур GeSi/Si [12], d-легированных квантовых ям [13] и сверхрешеток [14], а также на основе других сложных полупроводников [15, 16].
Вместе с тем, наиболее значительные успехи в области создания матричных фотодетекторов ИК-диапазона с высокими пороговыми характеристиками достигнуты на пути разработки высококачественных фотодиодов на основе HgCdTe, которые на сегодняшний день являются основным элементом для создания фокальных матриц.
Из материала Hg1-xCdxTe с х > 0,2 изготовляются фотодиоды на спектральный диапазон 8-14 мкм, как на основе n+-р [17-20], так и р+-n-переходов [4], причем наиболее отработанной является технология n+-р-переходов. Шум таких р-n-переходов является белым вплоть до частот порядка 1-10 Гц [4, 18, 20]. На основе высококачественных HgCdTe n+-р переходов разработаны крупноформатные матрицы и линейки [3, 5, 17-20]. Из Hg1-xCdxTe состава х > 0,3 также разработаны фотодиоды с малыми темновыми токами, что дало возможность повысить рабочую температуру крупноформатной фокальной матрицы на спектральный диапазон 3-5 мкм вплоть до уровня термоэлектрического охлаждения [2]. В этом заключается главное преимущество фотодетекторов на основе HgCdTe на спектральный диапазон 3-5 мкм перед фотодетекторами из InSb, рабочую температуру которых существенно повысить не удается.
В отличие от фокальных матриц на основе PtSi [9], гетеропереходов GeSi/Si [10], а также квантовых ям и сверхрешеток квантовая эффективность фокальных матриц на основе HgCdTe близка к единице. Фотодетекторы на основе квантовых ям и сверхрешеток к тому же обладают селективным по поляризации поглощением (нормально падающее излучение поглощается слабо) [13, 14, 21].
Пороговые характеристики квантовых фотодетекторов на основе HgCdTe, в принципе, лучше, чем болометрических фотоприемников. В квантовых фотодетекторах, например, при межзонном поглощении ИК-излучения, каждый поглощенный фотон генерирует электронно-дырочную пару, которая и определяет фототок. В тепловых фотоприемниках энергия поглощенного фотона перераспределяется между всеми подсистемами кристалла. Поэтому чувствительность тепловых приемников ниже, чем квантовых. Отметим также, что пороговые характеристики фотодиодов на основе Hg1-xCdxTe состава х > 0,2 лучше, чем у фоторезисторов на основе квантоворазмерных гетероструктур GaAs/AlGaAs [22].
Заметим, что попытки создания на основе узкозонных полупроводников фоточувствительных приборов с зарядовой связью (ПЗС) или с зарядовой инжекцией (ПЗИ) (успешно реализованные на основе Si [23, 24]) также натолкнулись на значительные сложности. Это связано с тем, что в узкозонных полупроводниках туннельный ток существенно ограничивает коэффициент переноса и быстродействие [25]. Кроме того, граница раздела узкозонный полупроводник-диэлектрик характеризуется достаточно высокой плотностью состояний, что естественно ухудшает пороговые характеристики таких матриц. Поэтому достигнутый сегодня формат ПЗС среднего ИК-диапазона на основе HgCdTe [26] существенно меньше, чем формат разработанных к настоящему времени гибридных матриц [2].
Таким образом, в обозримом будущем фотодиоды на основе HgCdTe, по-видимому, останутся основным элементом для создания крупноформатных фокальных матриц с высокими пороговыми характеристиками как среднего, так и дальнего ИК-диапазонов. При этом наиболее перспективным материалом для создания таких приборов являются эпитаксиальные слои HgCdTe, выращенные на подложках из CdTe, CdZnTe или альтернативных подложках [27, 28]. Обладая достаточно высокой однородностью электрофизических параметров такие слои, в отличие от объемных монокристаллов HgCdTe не требуют предварительной механической обработки поверхности, а изготовленные на их основе фотодиоды могут освещаться со стороны подложки, прозрачной для ИК-излучения.
Однако на пути реализации потенциальных преимуществ фокальных матриц длинноволнового ИК-диапазона имеются значительные трудности. Одна из них состоит в сложности получения эпитаксиальных слоев Hg1-xCdxTe состава х > 0,2 большой площади с высоким совершенством поверхности и сложности проведения стыковки с кремниевой микросхемой на большой площади. Однако главная трудность создания крупноформатных матриц на диапазон 8-12 мкм связана с высоким уровнем фонового излучения в таком длинноволновом ИК-диапазоне. Сильный фон приводит к быстрому переполнению накопительных емкостей, расположенных на кремниевой микросхеме, и тем самым обусловливает использование высокой тактовой частоты для считывания фотосигналов. Чем больше формат матрицы (точнее число элементов в ее строке), тем выше должна быть эта тактовая частота, а следовательно и шумовая полоса частот обрабатывающей электроники. Таким образом, чем больше формат матрицы, тем сильнее влияние шумов обрабатывающей электроники на ее пороговые характеристики. Это является принципиальной причиной, ограничивающей формат матриц длинноволнового ИК-диапазона, работающих в BLIP-режиме. Именно по этим причинам формат разработанных на сегодня фокальных ИК HgCdTe матриц [3-5] меньше, чем формат матриц на основе PtSi [9]. Для достижения максимальных пороговых характеристик матрицы большого формата необходимо обеспечить время накопления фотосигнала, соизмеримое с временем кадра.
Таким образом, разработка фокальных матриц длинноволнового ИК-диапазона, с большим временем накопления фотосигнала (в пределе, равном постоянной времени человеческого глаза) является чрезвычайно актуальной задачей.
В данной статье излагается физика работы, рассматриваются фотоэлектрические и пороговые характеристики новой гибридной фокальной матрицы на основе HgCdTe, которая обладает достаточно большим временем накопления. Статья построена следующим образом. В разд. 2 рассматривается архитектура и физика работы матрицы; в разд. 3 анализируется процесс накопления фотосигнала; в разд. 4 изучается зависимость ее чувствительности, обнаружительной способности, условия реализации BLIP-режима от конструктивных параметров, а также рассматривается метод подавления шумов предусилителя типа 1/f;
в разд. 5 приводятся результаты расчетов фотоэлектрических и пороговых характеристик таких матриц на основе Hg1-xCdxTe состава х > 0,2 и х > 0,3.
2. Архитектура и физика работы матрицы
Рассматриваемая гибридная фокальная матрица состоит из матрицы фоточувствительных р-n-переходов на основе эпитаксиальных слоев HgCdTe, соединенных с матрицей накопительных емкостей посредством индиевых столбиков (рис. 1).
Матрица фоточувствительных р-n-переходов освещается со стороны подложки. Мы уже отмечали, что в настоящее время наиболее хорошо отработана технология создания n+-р-переходов на основе Hg1-xCdxTe состава х > 0,2, причем темновой ток таких обратносмещенных р-n-переходов определяется диффузионным механизмом [17, 20]. Поэтому для определения предельных параметров предложенной нами перспективной фокальной матрицы длинноволнового ИК-диапазона мы для определенности будем рассматривать фотодиоды на основе n+-р-переходов (рис. 1).
Сечение ячейки матрицы накопительных емкостей плоскостью, параллельной шине Xj (см. рис.1), изображено на рис. 2. Каждая такая ячейка состоит из двух конденсаторов C1 и С2. Верхние обкладки этих конденсаторов образованы электродами 1 и 2 соответственно, а нижние их обкладки образованы общим
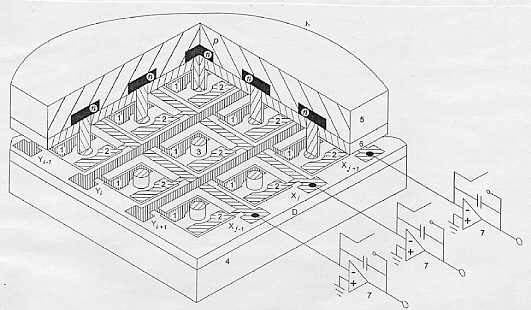
Рис. 1. Архитектура гибридной матрицы :
1 - электрод, соединенный с шиной столбца Yi; 2 - электрод, соединенный с шиной строки Xj;
3 - индиевый столбик; 4 - подложка матрицы накопительных емкостей; D - слой диэлектрика с
относительно высокой диэлектрической проницаемостью; 5 - подложка матрицы фотодиодов;
6 - пассивирующий диэлектрический слой, р и п - области узкозонного полупроводника р- и n- типа проводимости,
соответственно; 7 - зарядовый усилитель. (Показан режим считывания, когда ключи в цепях
обратной связи операционных усилителей разомкнуты)
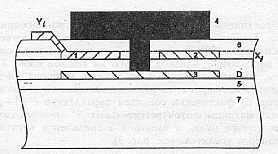
Рис. 2. Структура ячейки матрицы накопительных емкостей:
1 - электрод, соединенный с шиной столбца Yi и образующий верхнюю обкладку
конденсатора С1 ; 2 - электрод, соединенный с шиной строки Хj и образующий
верхнюю обкладку конденсатора С2; 3 - общий металлический электрод,
соединенный с индиевым столбиком 4 и образующий нижние обкладки конденсаторов
С1 и С2; 5 и 6 - слои диэлектрика; 7 - подложка матрицы накопительных
емкостей; D - слой диэлектрика с относительно высокой e
металлическим электродом 3. Этот общий нижний электрод соединен с сильно легированной n+-областью фоточувствительного n+-р-перехода посредством индиевого столбика. Таким образом, конденсаторы С1 и С2 занимают всю площадь ячейки матрицы накопительных емкостей, а функции элемента коммутации, как будет ясно из дальнейшего, выполняет сам фоточувствительный n+-p-переход. Такое оптимальное конструктивное решение обеспечивает время накопления фотосигнала в рассматриваемой матрице много большее, чем в разработанных ранее гибридных матрицах [2-5], в которых значительную часть площади ячейки кремниевой микросхе- мы занимают транзисторные ключи.
Отметим, что максимальный заряд плоского конденсатора равен Q = CV = =ee0AEmax, где e и e0 - диэлектрическая проницаемость диэлектрика и электрическая постоянная, соответственно; Emax = V/d - поле пробоя диэлектрика; А - площадь конденсатора С; d - толщина диэлектрического слоя. Для большинства диэлектриков Emax > 106 В/см, поэтому пробивное напряжение накопительных емкостей на основе сверхтонких диэлектрических слоев довольно мало (20). Для повышения величин емкостей конденсаторов С1 и С2 рассматриваемая структура металл-диэлектрик-металл может быть изготовлена на основе диэлектрика с достаточно высокой диэлектрической проницаемостью, например TiO2 [29, 30]. Возможность применения таких диэлектриков, получение которых требует, как правило, достаточно высоких температур отжига, недопустимых для HgCdTe, связана с тем, что матрицы фоточувствительных и накопительных элементов в гибридной конструкции изготовляются раздельно. Отметим, что в случае, когда матрица накопительных емкостей изготовляется на подложке из диэлектрика, емкость шины Xj пренебрежимо мала.
Большое время накопления фотосигнала в рассматриваемой матрице обусловлено эффективным использованием площади ячейки матрицы накопительных элементов и применением диэлектриков с относительно высокой диэлектрической проницаемостью. В этом заключается главное преимущество предложенной нами фокальной матрицы по сравнению с разработанными ранее гибридными фокальными матрицами на основе HgCdTe [2-5] и планарной матрицей на основе InSb [31].
Итак, каждая ячейка предложенной нами фокальной матрицы состоит из одного фоточувствительного р-n-перехода и двух емкостей. Структура соединения фоточувствительных р-n-переходов и накопительных ячеек в рассматриваемой матрице показана на рис. 1 и рис. 3. Все электроды 1 каждого из столбцов матрицы накопительных элементов соединены между собой узкими проводящими перемычками (шинами) Yi, а все электроды 2 каждой из строк этой матрицы соединены между собой шинами Хj, изолированными от шин Yi. Каждая из шин Хj соединена с инвертирующим входом соответствующего операционного усилителя (ОУ), который работает в режиме усилителя заряда и поддерживает напряжение, близкое к нулю на каждой шине Хj. Слой полупроводника р-типа, выполняющий роль подложки матрицы фоточувствительных n+-р-переходов, заземлен, т. е. на нем поддерживается напряжение, равное нулю. Конденсатор С2 фактически соединен параллельно с n+-р-переходом, так как на подложке матрицы фоточувствительных n+-р-переходов поддерживается напряжение, равное нулю, а электрод 2 соединен с виртуальным нулем на входе операционного усилителя (см. рис. 3).
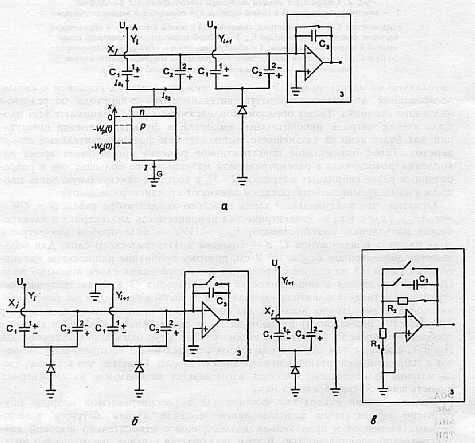
Рис. 3. Эквивалентная схема матрицы в режиме накопления (а),
в режиме считывания (b), и в режиме измерения ЭДС шума ОУ (в):
1 - электрод 1-й ячейки матрицы накопительных емкостей, соединенный с шиной столбца Yi ; 2 - электрод
2-й ячейки матрицы накопительных емкостей, соединенный с шиной строки Хj ; 3 - зарядовый усилитель,
в котором ключ в цепи обратной связи ОУ замкнут в режиме накопления (см. рис. а) и разомкнут
в режиме считывания (см. рис. б); C3 - емкость в цепи обратной связи ОУ; U - напряжение,
подаваемое на столбец в режиме накопления. Знаками + и - обозначены знаки зарядов, возникающих на
соответствующих обкладках конденсаторов С1 и С2; Iс1, Ic2 - токи смещения, протекающие через
конденсаторы С1 и С2, соответственно: I= Ajc (-Wp(0),t) - ток проводимости в точке - Wp(0);
R1 и R2 - малые сопротивления, подсоединенные к ОУ в режиме измерения ЭДС-шума
На рис. 3, а, б изображены эквивалентные схемы матрицы в режимах накопления и считывания, соответственно. Заметим, что аналогичная электронная схема была апробирована вначале на основе дискретных радиотехнических элементов и фотодиодов из InSb и Si [32], а затем была использована для создания интегральной фокальной матрицы среднего ИК-диапазона на основе InSb [31].
Накопление фотосигнала происходит непрерывно и одновременно на всех ячейках фокальной матрицы, а считывание осуществляется сразу со всего выбранного столбца и происходит за время, намного меньше времени накопления. При этом все столбцы опрашиваются за время накопления фотосигнала.
В начальный момент режима накопления на все шины Yi (см. рис. 1,3, а), т. е. на все электроды 1, подается напряжение U > 0. Это напряжение практически мгновенно перераспределится между емкостью С1 и емкостью параллельно соединенных р-n- перехода и конденсатора С2. В результате р-n-переход сместится в обратном направлении, а на электроде 1 возникнет положительный заряд, на электроде 2 - отрицательный.
Отметим, что время накопления фотосигнала в данной матрице, как будет видно из дальнейшего, тем больше, чем больше падение напряжения на р-n-переходе и на емкостях С1 и С2 в начальный момент времени. Максимальная величина падения напряжения на р-n-переходе ограничена его пробоем, а максимальное напряжение на конденсаторах С1 и С2 ограничено пробоем диэлектрика, на основе которого изготовлены эти емкости (см. рис. 2).
Под действием сигнального и фонового излучения, а также тепла в высокоомной р- области обратносмещенного n+-р-перехода генерируются электронно-дырочные пары. В результате фототока и темнового тока р-n-перехода происходит разрядка его емкости и изменение напряжений на емкостях С1 и С2. При этом абсолютная величина напряжения на емкости С1 увеличивается, а на С2 - уменьшается, и чем больше фотонов попадает на р-n-переход, тем сильнее изменение напряжений на емкостях С1 и С2 в данной ячейке. Математическое описание этого процесса, определяющего все основные параметры матрицы, дано в разд. 3. Здесь же мы подчеркнем, что изменение напряжения на емкости С2 пропорционально числу фотонов, упавших на данную ячейку, т. е. по существу является фотосигналом. Отсюда вытекает, что для обеспечения линейного режима напряжение на р-n-переходе под действием излучения не должно уменьшаться до нуля, а тем более менять знак.
Считывание накопленного на емкостях фотосигнала происходит одновременно со всех ячеек выбранного столбца Yi. Для этого на шину Yi подается нулевой потенциал и размыкаются ключи в цепях обратной связи всех зарядовых усилителей (см. рис. 3, б). Подача на шину Yi нулевого потенциала означает заземление электродов 1 емкостей С1 i-го столбца (см. рис. 1). Рассмотрим этот процесс на примере ji-й ячейки, находящейся на пересечении j-й строки и i-го столбца (см. рис. 3, б).
При заземлении электрода 1 опрашиваемой ячейки происходит подключение напряжения U1 емкости С1 к р-n-переходу. В результате чего р-n-переход, который и после воздействия излучения слабо смещен в обратном направлении, переключается в прямом направлении напряжением U1 порядка нескольких вольт. Это приведет к быстрой разрядке конденсатора С1 через прямосмещенный р-n-переход и установлению на нем напряжения, близкого к нулю. Одновременно с разрядкой конденсатора С1 начинается разрядка конденсатора С2 через прямосмещенный р-n- переход и зарядовый усилитель, точнее через емкость С3 в цепи обратной связи операционного усилителя (см. рис. 3). Таким образом, заряд конденсатора С2, который зависит от интенсивности светового сигнала, действительно является мерой величины этого сигнала.
Подчеркнем существенный момент, что изложенный процесс считывания сигнала с i- го столбца практически не влияет на процесс накопления фотосигнала в ячейках всех остальных столбцов. Это связано с тем, что как в процессе считывания, так и в процессе накопления напряжение на всех шинах Хj остается равным нулю с точностью до нескольких милливольт. Однако процесс накопления сигнального и фонового зарядов в ячейках, принадлежащих какой-либо одной строке, оказывает влияние на процесс считывания накопленного заряда с опрашиваемой ячейки данной строки и может в принципе привести к некоторому (примерно в раз) ухудшению пороговых характеристик рассматриваемой фокальной матрицы.
Из изложенного также следует, что процесс считывания не связан с переносом накопленного заряда вдоль границы раздела полупроводник-диэлектрик между пространственно разнесенными электродами. Поэтому шум, связанный со случайностью процессов захвата и выброса носителей с поверхностных состояний на границе раздела полупроводник-диэлектрик, в данной матрице (в отличие от фото-ПЗС и -ПЗИ матриц [33]) не является определяющим. Это одно из главных преимуществ рассматриваемой гибридной фокальной матрицы по сравнению с фото-ПЗС и -ПЗИ матрицами.
3. Анализ процесса накопления
Мы уже отмечали, что в рассматриваемой фокальной матрице фоточувствительные р-n-переходы освещаются со стороны слабо легированной р-области. Поэтому распределение концентрации неравновесных носителей и потенциала по плоскости р-n- перехода является однородным, и математическое описание процессов накопления в ячейке фокальной матрицы можно проводить в рамках одномерной модели с использованием эквивалентной схемы, изображенной на рис. 3, а, б.
Отметим, что в фотодиодах на основе узкозонных полупроводников могут возникать туннельные токи утечки в локальных областях по периметру сильнолегированной области вблизи выхода р-n-перехода к границе раздела полупроводник-диэлектрик [34-36]. Эти поверхностные туннельные токи и взрывные шумы р-n-переходов на основе узкозонных полупроводников, как показано в работах [37-39], связаны с относительно большим встроенным зарядом диэлектрика. Однако сегодняшний уровень технологии позволяет изготовить р-n-переходы на основе Hg1-xCdxTe состава х > 0,2, в которых при обратном смещении будет доминировать диффузионный ток [4, 17, 20].
Мы уже упоминали выше, что в процессе накопления на шине Yi поддерживается напряжение U, большее нуля. Однако поскольку напряжение такой полярности смещает р-n-переход в обратном направлении, для дальнейшего анализа процесса накопления удобно считать, что потенциал точки А (см. рис. 3, а) равен 0, а потенциал точки G равен U.
В одномерном случае уравнение непрерывности полного тока есть:
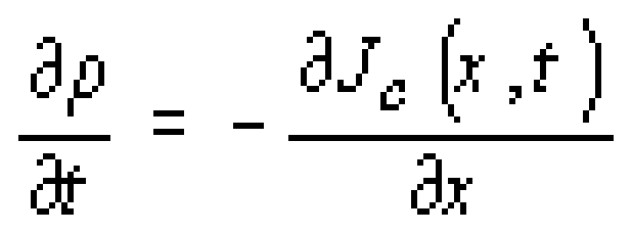
где r - плотность заряда; хc(x, t) - плотность тока проводимости; ось х перпендикулярна плоскости р-n-перехода.
Проинтегрируем (1) по x от точки х = -Wp(0) (границы области пространственного заряда (ОПЗ) в р-области в начальный момент времени t = 0) на рис. 3, а до точки х = 0, где Na = Nd (металлургическая граница р-n-перехода), и умножим его на площадь р-n-перехода А. В результате получим:
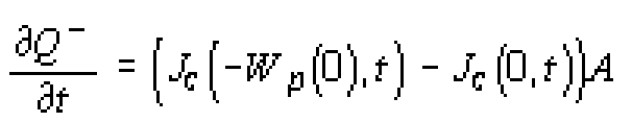
Здесь учтено, что интеграл от левой части уравнения (1), умноженный на A, есть производная по времени отрицательного заряда Q- в р-области ОПЗ р-n-перехода.
Граница квазинейтральной р-области с ОПЗ в момент времени t = 0 (точка х = - Wp(0) на рис. 3, а) в другие моменты времени t > 0 находится в квазинейтральной области р-типа. Поэтому напряженность электрического поля в ней во все моменты времени равна нулю и следовательно равен нулю ток смещения, т. е. полный ток в этой точке равен току проводимости. Тогда из закона Кирхгофа следует, что
Aх(- Wp(0),t) + IC2 = IС1,
где IС1 , IС2 - токи смещения, протекающие через конденсаторы С1 и С2 (см. рис. 3, a), которые соответственно равны
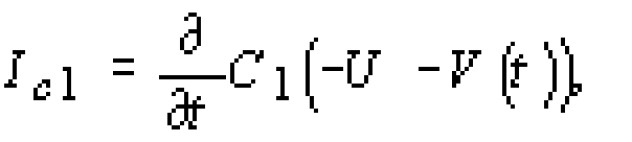
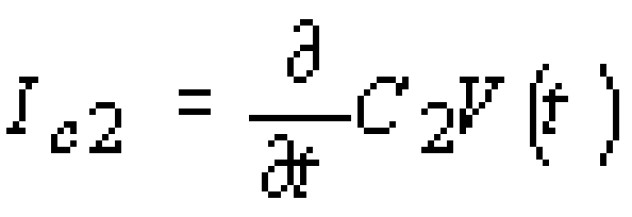
Заметим, что согласно сделанному в начале этого пункта допущению, -U потенциал точки G (см. рис. З, а), a V(t) - напряжение на р-n-переходе меньше 0. Из (3) и (4) следует, что
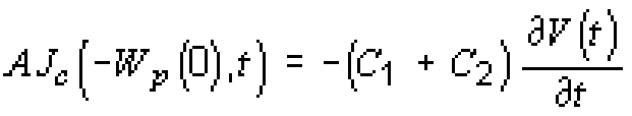
Отметим, что время накопления в рассматриваемой фокальной матрице достаточно велико по сравнению с временем жизни неравновесных носителей в Hg1-xCdxTe p-типа состава х > 0,2, которое составляет величину порядка микросекунды при Т = 77 К. Это позволяет рассматривать процесс накопления фотоносителей как квазистационарный и, в частности, для области р-типа использовать стационарное диффузионное уравнение для электронов. Возможность отбрасывания производной по времени от концентрации неосновных носителей (dn/dt) в этом диффузионном уравнении имеет простой физический смысл. В процессе накопления на р-n-переходе поддерживается обратное смещение, поэтому концентрация неосновных носителей - электронов в квазинейтральной области p-типа остается экспоненциально малой по сравнению с равновесной. На границе ОПЗ - квазинейтральная область p-типа накапливаются основные носители - дырки, а электроны накапливаются на границе ОПЗ - квазинейтральная область n-типа. Таким образом накопление темнового и фототока происходит на барьерной емкости р-n-перехода, а не на диффузионной емкости, которая мала при обратном смещении р-n-перехода [40].
Известно [33], что для стационарного случая плотность электронного тока на границе ОПЗ р-n-перехода и квазинейтральной области р-типа хn(- Wp(t)можно записать в виде
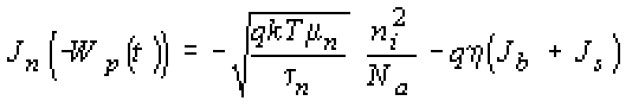
где q - заряд электрона; k - постоянная Больцмана; Т - температура; mn - подвижность электронов; tn - время жизни электронов; ni - собственная концентрация; Na - концентрация акцепторов в р-области (подложке матрицы фоточувствительных р-n-переходов); h - квантовая эффективность поглощения ИК излучения; хb и хs - плотности потока фотонов фонового и сигнального излучения, соответственно; Wp(t) - ширина ОПЗ в области р-типа в момент времени t (см. рис 3, а).
Предположим, что в рассматриваемом р-n-переходе доминирует диффузионный ток, а генерация и рекомбинация носителей в ОПЗ мала. Более того, толщина квазинейтральной области р-типа намного больше характерной длины поглощения ИК- излучения, поэтому сигнальное и фоновое излучение полностью поглощается в этой области, а фотогенерацией в ОПЗ можно пренебречь. Отсюда следует, что плотности электронного и дырочного токов в ОПЗ постоянны, т. е. выполняется равенство хn(0,t) = хn(- Wp(t),t). В силу того, что концентрация донорной примеси в n+-области Nd намного больше концентрации акцепторной примеси в области р-типа (Nd >> Na), основной вклад в темновой ток n+-р-перехода вносит электронный ток области р-типа. Поэтому на металлургической границе р-n-перехода (в точке х = 0 на рис. 3, а) плотность тока электронов намного больше плотности тока дырок (хn(0,t) >> (хp(0,t)), т. е. ток проводимости практически равен диффузионному току электронов:
хc(0,t) = хn(0,t) = хn(- Wp(t),t) .
Подставляя уравнения (5) и (7) в (2) и используя (6), получим уравнение, описывающее процесс накопления заряда в ячейке рассматриваемой фокальной матрицы:
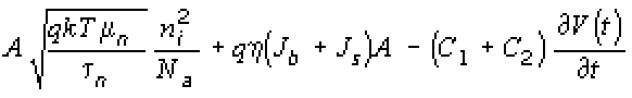
Здесь производная по времени отрицательного заряда, накапливаемого на границе ОПЗ с квазинейтральной p-областью, по определению равна [40]:
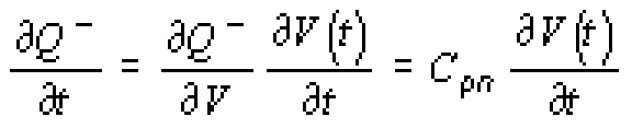
где Сpn - барьерная емкость р-n-перехода.
Поясним теперь физический смысл уравнения (8). В процессе накопления термо- и фотогенерируемых носителей происходит перезарядка как емкости р-n-перехода (с этим процессом связан член dQ-/dt), так и емкостей С1 и С2 (с этим процессом связан член (С1 + C2) dV(t)/dt). За счет совместной перезарядки емкости р-n-перехода и емкостей С1 и С2 в рассматриваемой матрице можно достичь времен накопления намного больших, чем для обычного режима накопления, когда перезаряжается только барьерная емкость р-n-перехода [33]. Для достижения большого времени накопления фотосигналов необходимо чтобы С1 + С2 >> Сpn. При выполнении этого условия уравнение (8), описывающее процесс накопления заряда в ячейке рассматриваемой фокальной матрицы примет вид:
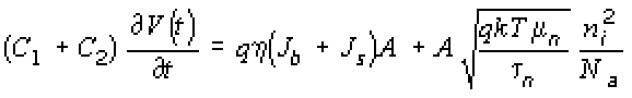
Отметим, что при записи уравнения (10) мы пренебрегли туннельным током р-n- перехода, так как предполагаем, что приложенное к нему напряжение, в начальный момент времени, а следовательно, и во все остальные, выбирается меньше напряжения его пробоя.
Решение уравнения (10) при условии, что в момент времени t = 0 напряжение на р-n-переходе было равно V(0), примет вид
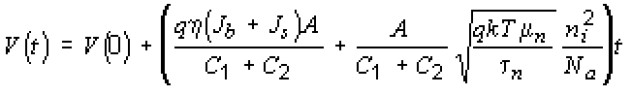
4. Фотоэлектрические и пороговые характеристики
Основной фотоэлектрической характеристикой фокальных матриц, работающих в режиме накопления, является зарядовая чувствительность SQ, по определению равная:
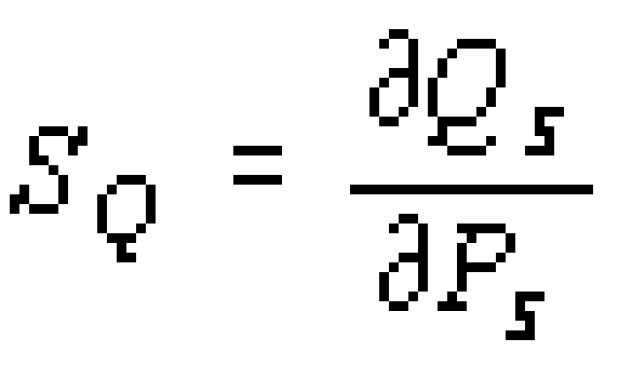
где Qs - сигнальный заряд, Ps - мощность сигнального излучения.
В рассматриваемой фокальной матрице сигнальным зарядом является заряд QС2 на конденсаторе C2, равный C2 V(t). Для простоты будем считать, что падающее излучение монохроматическое, т. е. Ps = hwAхs . Тогда из (11) получим:
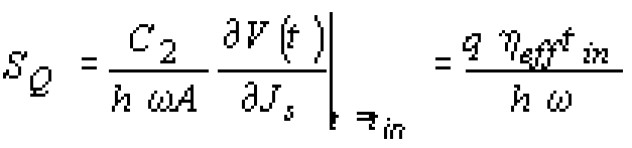
где hw - энергия кванта падающего излучения; tin - время накопления фотосигнала; heff - величина, определяющая эффективность накопления фотосигнала в данной матрице:
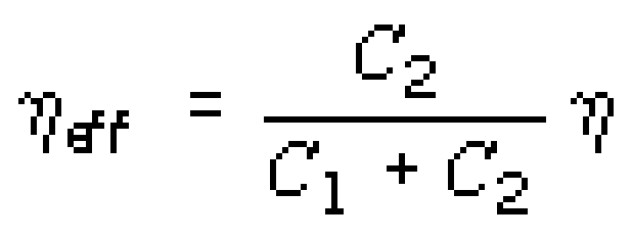
Выражение (14) отражает эффект уменьшения квантовой эффективности, обусловленный тем, что в рассматриваемой фокальной матрице накопление фотосигнала происходит на емкостях C1 и C2, а считывание лишь с емкости С2. Для того чтобы сделать величину heff максимально близкой к квантовой эффективности поглощения емкости С1 и С2 должны быть выбраны так, чтобы:
С2 >> С1.
Рассмотрим теперь условия, при которых неравенство (15) может быть реализовано, а также получим соотношения между емкостями С1 и С2, которые вытекают из ограничений на величины напряжений V(0) и U, налагаемых пробоем фоточувствительного р-n-перехода и диэлектрика, на основе которого изготовлена емкость С1 соответственно.
Очевидно, что напряжение, подаваемое в начальный момент времени t = 0 на р-n-переход должно быть меньше напряжения его пробоя Vbpn:
ъV(0) ъ < Vbpn,
а напряжение на конденсаторе С1 в момент окончания накопления t = tin должно быть меньше напряжения пробоя диэлектрика Vb, на основе которого изготовлен этот конденсатор:
U - gъV(0) ъ < Vb,
здесь U - внешнее напряжение, поданное на электроды 1 (см. рис. 1), т. е. на шины Yi (рис. 3, а), а g - параметр, который задается соотношением g = V(tin)/V(0); его значения лежат в интервале между 0 и 1.
Принимая во внимание, что в рассматриваемой матрице С2 >> Сpn , можно записать, что в момент времени t = 0 напряжения на емкостях С1 и С2 удовлетворяют очевидному соотношению:
С1(U - ъV(0) ъ) = С2 фV(0) ф.
Определяя величину U из (18) и подставляя ее в (17), получим неравенство:
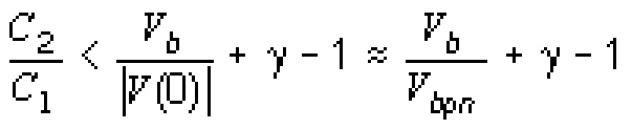
Из (19) следует, что условие высокой эффективности накопления фотосигнала (15) может быть выполнено только тогда, когда напряжение пробоя диэлектрика намного больше напряжения пробоя р-n-перехода, т. е. когда
Vb >> Vbpn .
Отметим, что напряжение пробоя р-n-переходов на основе Hg1-xCdxTe состава х > 0,3 примерно равно 5 В, а состава х > 0,2-0,5 В [20]. Поэтому, согласно (20), квантовая эффективность рассматриваемой фокальной матрицы длинноволнового ИК-диапазона будет близка к квантовой эффективности поглощения, если напряжение пробоя конденсатора С1 будет превышать 5 В. Это соответствует полю пробоя, превышающему
5·105 В/см при толщине диэлектрика 1000 A°. Для фокальных матриц среднего ИК-диапазона, как будет показано ниже, необходимы значительно меньшие величины емкостей С1 и С2 , чем для матриц длинноволнового ИК-диапазона, поэтому толщина диэлектрика, на основе которого изготовлен конденсатор C1, может превышать величину 1000 A°. Кроме того, TiO2 обладает весьма значительным полем пробоя
(1-5)·106 В/см [30]. Таким образом, при надлежащем выборе диэлектриков для конденсаторов С1 и С2 можно добиться того, что квантовая эффективность рассматриваемой фокальной матрицы будет близка к единице.
Параметрами, характеризующими пороговые характеристики фотодетекторов, являются мощность, эквивалентная шуму NEP, и обнаружительная способность D[41], которые для систем с накоплением фотосигнала равны:
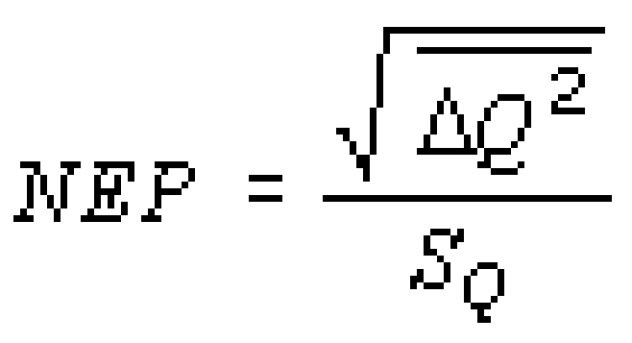
где 
- дисперсия флуктуаций заряда на выходе прибора.
При рассмотрении пороговых характеристик матрицы необходимо учитывать шумы, связанные с флуктуациями темнового тока фоточувствительного р-n-перехода и фонового излучения, а также шум зарядового усилителя и так называемый kTC-шум [33].
Отметим, что время считывания фотосигнала в матрице достаточно мало (см. разд. 2), поэтому шум усилителя типа 1/f не играет существенной роли в процессе считывания. Напротив, время накопления фотосигнала велико и шум усилителя типа 1/f может определять пороговые характеристики матрицы. Для достижения высоких пороговых характеристик матрицы предлагаем схему подавления шума усилителя типа 1/f . В режиме накопления отсоединим зарядовые усилители от строк матрицы и заземлим все шины Хj (см. рис. 3, в). В этом случае процесс накопления в ячейках любой j-й строки никак не изменится (см. разд. 2), но шумы усилителя не будут влиять на пороговые характеристики матрицы. Однако при считывании накопленного сигнала зарядовые усилители подключаются к строкам матрицы.
Пусть строка матрицы содержит n ячеек, подключенных к одному зарядовому усилителю. В этом случае время считывания фотосигнала в матрице не может превышать tin/n. Уменьшение времени считывания приведет к возрастанию полосы частот усилителя и тем самым к увеличению его шумов. Пусть шум усилителя намного меньше шумов фонового излучения, т. е. условие BLIP-режима в матрице (см. уравнение (27) ниже) выполняется с большим запасом. Эта ситуация может реализовываться, например, в матрицах не слишком большого формата, в которых время считывания фотосигнала не слишком мало. В таких матрицах время считывания фотосигнала может быть уменьшено по сравнению с tin/n, так как некоторое увеличение полосы частот усилителя не слишком сильно повлияет на пороговые характеристики. Таким образом, в таких “малоформатных” матрицах большую часть времени накопления шины строк Хj могут быть заземлены, и влияние шумов усилителя типа 1/f на пороговые характеристики будет крайне малым.
В матрицах большого формата время считывания не может быть существенно меньше tin/n и усилители подключены к строкам матрицы практически все время накопления. Однако и в этом случае шум усилителя типа 1/f может быть подавлен. Для этого нужно после считывания заряда с какой либо ячейки отключить шины строк Хj от операционных усилителей на короткое время t < tin/n и заземлить их. В течение этого времени мы можем измерить шум каждого операционного усилителя не нарушая процесса накопления сигнала. Для этого подключим малое сопротивление R1 между инвертирующим и неинвертирующим входами каждого операционного усилителя, а R2 - в цепь его обратной связи (рис. 3, в). Заметим, что R1 и R2 могут быть сопротивлениями открытых транзисторных ключей. В результате получим обычную схему измерения электродвижущей силы (ЭДС) шума операционного усилителя [42]. В принципе за время накопления измерение шума можно выполнить n -1 раз. Это позволяет усреднить полученную выборку по одному или нескольким временам накопления. В результате получим ЭДС шума усилителя, обусловленную низкочастотными флуктуациями (с граничной частотой, соответствующей периоду усреднения). Это позволяет исключить вклад низкочастотных шумов усилителя в накопленный сигнал при дальнейшей обработке сигнала.
Мы уже отмечали выше, что спектр шума высококачественных HgCdTe р-n-переходов является белым вплоть до частот порядка 1 - 10 Гц [4, 18, 20]. В тоже время kTC-шум может быть устранен посредством использования метода двойной коррелированной выборки [33]. Кроме того, в современных фоточувствительных р-n-переходах на основе Hg1-xCdxTe при не слишком малом угле зрения на фон фоновый ток намного больше темнового [3, 17, 20]:
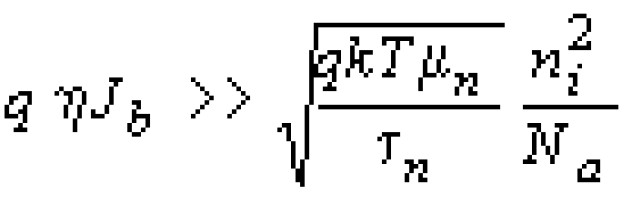
Это означает также [41], что шум таких фотодиодов в основном определяется флуктуациями фонового излучения, т. е. для отдельного фотодиода выполнено условие BLIP-режима. Поэтому при расчете пороговых характеристик рассматриваемой фокальной матрицы будем учитывать только шум, связанный с флуктуациями фонового излучения и шум зарядового усилителя. Эти шумы не коррелированы, поэтому суммарная дисперсия флуктуаций заряда на выходе прибора равна сумме дисперсий каждого шума:
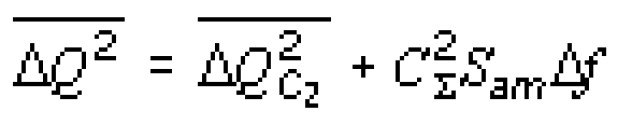
где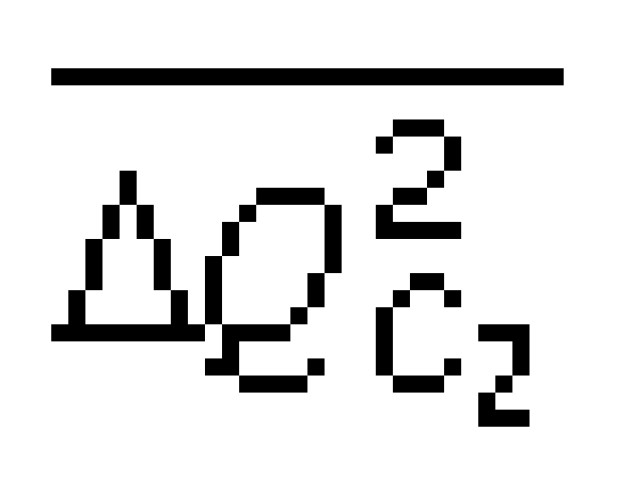 
- дисперсия флуктуаций заряда на конденсаторе С2, определяемая флуктуациями фонового излучения, в момент времени tin, который соответствует окончанию процесса накопления; C2S Sam Df - дисперсия флуктуаций заряда, определяемых шумом зарядового усилителя; Df - полоса частот усилителя; CS - суммарная емкость, подключенная ко входу зарядового усилителя; Sam - спектральная плотность шума усилителя. Отметим, что второе